Brand Logo Walter Teng.

100 Same Tree - Easy

Problem:

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

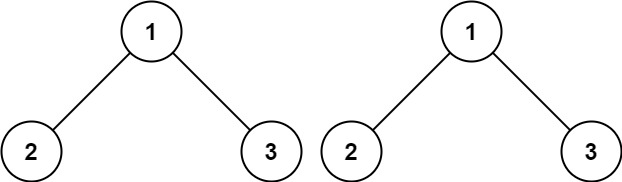
Input: p = [1,2,3], q = [1,2,3] Output: true

Example 2:

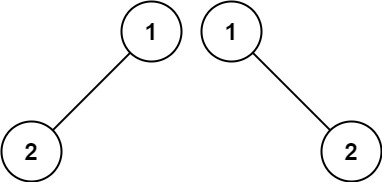
Input: p = [1,2], q = [1,null,2] Output: false

Example 3:

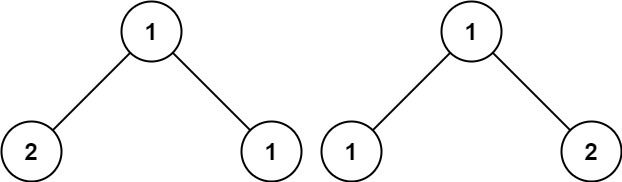
Input: p = [1,2,1], q = [1,1,2] Output: false

Constraints:

  • The number of nodes in both trees is in the range [0, 100].
  • -104 <= Node.val <= 104

Problem Analysis:

  1. High-Level Strategy:

    • The function isSameTree takes two binary trees p and q as input parameters.
    • It checks if both trees are identical in structure and node values recursively.
    • It first checks if both p and q are None, indicating the end of a branch, and returns True.
    • If one of them is None while the other is not, it means the trees are not identical, so it returns False.
    • If neither of the trees is None, it checks if the values of the current nodes of p and q are equal.
    • If the values are equal, it recursively checks the left and right subtrees of both trees.
    • The recursion continues until it reaches the leaf nodes or finds a mismatch in node values, at which point it returns False.
    • If the recursion reaches the end without finding any mismatches, it returns True, indicating that both trees are identical.

  2. Complexity:

    • Let's denote m as the number of nodes in tree p and n as the number of nodes in tree q.
    • In the worst case scenario, the function will have to traverse all nodes in both trees to determine whether they are identical.
    • Therefore, the time complexity of this solution is O(min(m, n)), as it will stop traversing as soon as it finds a mismatch.
    • The space complexity is O(min(m, n)) as well, due to the recursive calls made on the stack.

Solutions:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        if not p and not q:
            return True
        if not p or not q:
            return False
        return (p.val==q.val) and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right);

Similar Questions