1496 Path Crossing - Easy

Problem:

Given a string path, where path[i] = 'N', 'S', 'E' or 'W', each representing moving one unit north, south, east, or west, respectively. You start at the origin (0, 0) on a 2D plane and walk on the path specified by path.

Return true if the path crosses itself at any point, that is, if at any time you are on a location you have previously visited. Return false otherwise.

Example 1:

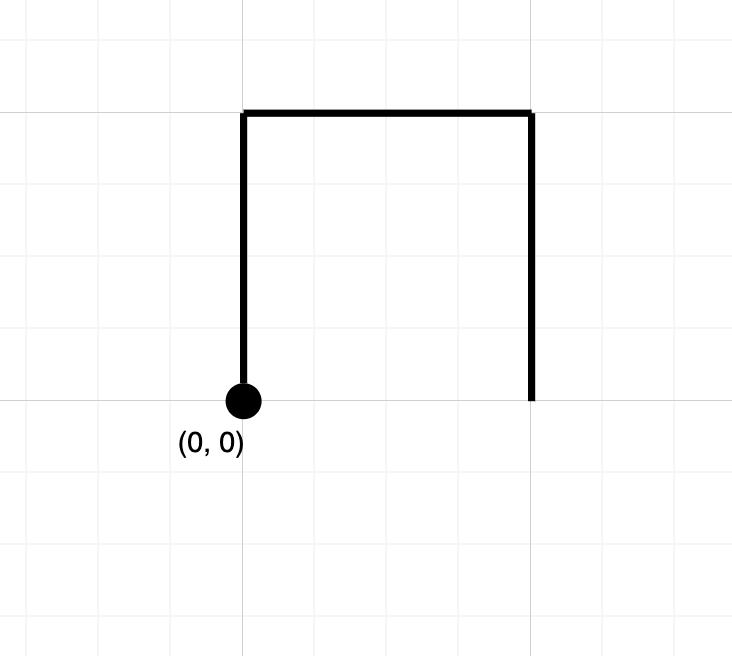
Input: path = "NES" Output: false Explanation: Notice that the path doesn't cross any point more than once.

Example 2:

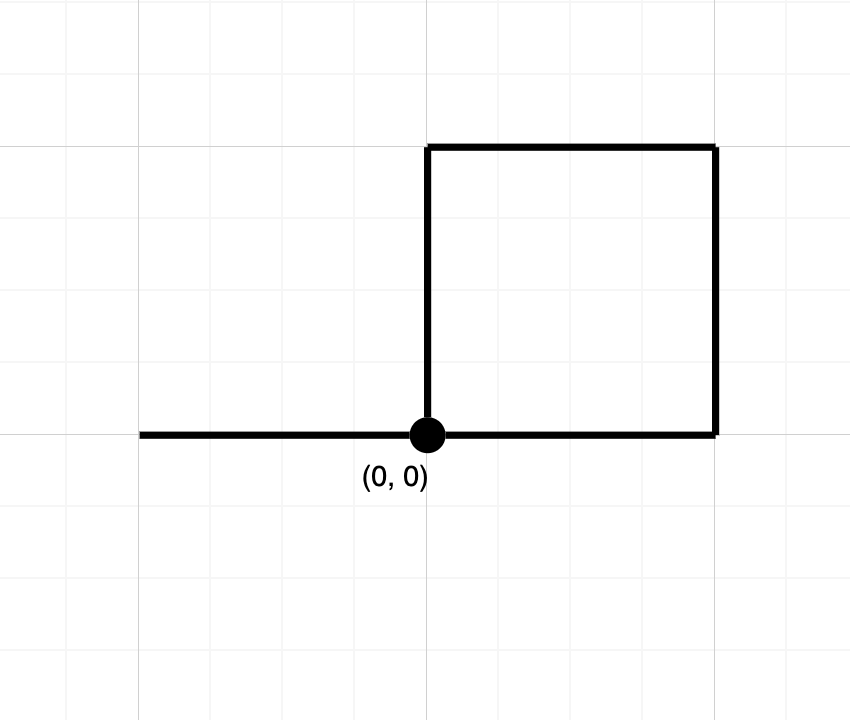
Input: path = "NESWW" Output: true Explanation: Notice that the path visits the origin twice.

Constraints:

• 1 <= path.length <= 104
• path[i] is either 'N', 'S', 'E', or 'W'.

Problem Analysis:

High-Level Strategy:

• The solution uses a set to keep track of visited points as the path progresses.
• It iterates through the given path string, updating the current position based on the direction specified in the path.
• At each step, it checks whether the current position has been visited before. If yes, it indicates a crossing path, and the function returns True.
• If the entire path is traversed without any revisits, the function returns False, indicating no crossing.

Complexity:

• Let n be the length of the path.
• The function iterates through the path string once, performing constant time operations for each step.
• Therefore, the time complexity is O(n).
• The set visited stores at most n distinct points, so the space complexity is also O(n).

Solutions:

class Solution:
    def isPathCrossing(self, path: str) -> bool:
        dir = {
            "N": [0,1],
            "S": [0, -1],
            "E": [1,0],
            "W": [-1, 0]
            }
        
        visited = set()
        x, y = 0, 0
        for i in path:
            visited.add((x,y))
            dx, dy = dir[i]
            x, y = x + dx, y + dy
            if (x,y) in visited:
                return True
        
        return False

Similar Questions