Brand Logo Walter Teng.

1561 Maximum Number of Coins You Can Get - Medium

Problem:

There are 3n piles of coins of varying size, you and your friends will take piles of coins as follows:

  • In each step, you will choose any 3 piles of coins (not necessarily consecutive).
  • Of your choice, Alice will pick the pile with the maximum number of coins.
  • You will pick the next pile with the maximum number of coins.
  • Your friend Bob will pick the last pile.
  • Repeat until there are no more piles of coins.

Given an array of integers piles where piles[i] is the number of coins in the ith pile.

Return the maximum number of coins that you can have.

Example 1:

Input: piles = [2,4,1,2,7,8] Output: 9 Explanation: Choose the triplet (2, 7, 8), Alice Pick the pile with 8 coins, you the pile with 7 coins and Bob the last one. Choose the triplet (1, 2, 4), Alice Pick the pile with 4 coins, you the pile with 2 coins and Bob the last one. The maximum number of coins which you can have are: 7 + 2 = 9. On the other hand if we choose this arrangement (1, 2, 8), (2, 4, 7) you only get 2 + 4 = 6 coins which is not optimal.

Example 2:

Input: piles = [2,4,5] Output: 4

Example 3:

Input: piles = [9,8,7,6,5,1,2,3,4] Output: 18

Constraints:

  • 3 <= piles.length <= 105
  • piles.length % 3 == 0
  • 1 <= piles[i] <= 104

Problem Analysis:

  • The high-level strategy of this solution is to sort the piles array in ascending order and then select every third element, starting from the last third of the array, considering every second element in the selected portion.
  • so that we can maximize the total number of coins you can get.

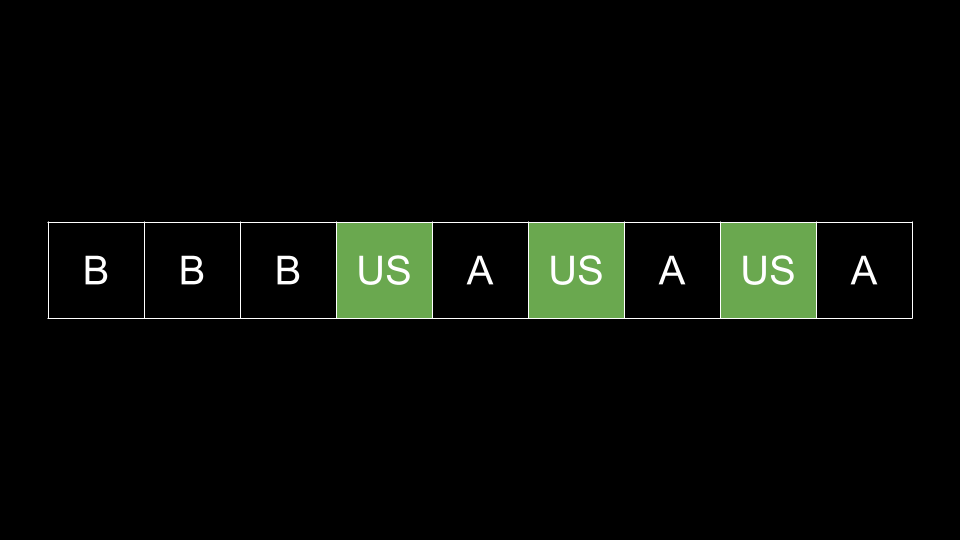
1561-1.png

For instance, in example 3, an unsorted array [9,8,7,6,5,1,2,3,4] gives out 8+5+3=16 which is not the best case for us.

We want a greedy approach where the piles are sorted as follows:

  1. [9,8,1]
  2. [7,6,2]
  3. [5,4,3]

In this case, we can get 8+6+4=18 giving us the answer/

  • Time Complexity:

    • O(N log N) due to the sorting operation.
      • The primary operation is sorting the piles array, which has a time complexity of O(N log N), where N is the length of the piles array.

  • Space Complexity:

    • O(1) - Constant space.
      • The space complexity is constant because the algorithm doesn't use additional data structures whose size depends on the input size. Sorting is typically an in-place operation. The slicing operation also uses constant space as it produces a new view on the existing array without creating a copy.

Solutions:

class Solution:
    def maxCoins(self, piles: List[int]) -> int:
        piles.sort()
        res = 0

        for i in range(len(piles) // 3, len(piles), 2):
            res += piles[i]
        
        return res

or

class Solution:
    def maxCoins(self, piles: List[int]) -> int:
        return sum(sorted(piles)[len(piles) // 3::2])

Similar Questions