1578 Minimum Time to Make Rope Colorful - Medium

Problem:

Alice has n balloons arranged on a rope. You are given a 0-indexed string colors where colors[i] is the color of the ith balloon.

Alice wants the rope to be colorful. She does not want two consecutive balloons to be of the same color, so she asks Bob for help. Bob can remove some balloons from the rope to make it colorful. You are given a 0-indexed integer array neededTime where neededTime[i] is the time (in seconds) that Bob needs to remove the ith balloon from the rope.

Return the minimum time Bob needs to make the rope colorful.

Example 1:

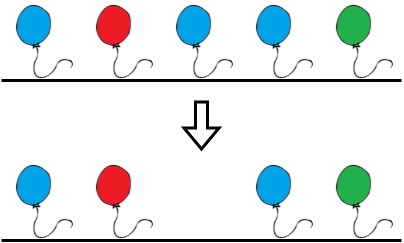
Input: colors = "abaac", neededTime = [1,2,3,4,5] Output: 3 Explanation: In the above image, 'a' is blue, 'b' is red, and 'c' is green. Bob can remove the blue balloon at index 2. This takes 3 seconds. There are no longer two consecutive balloons of the same color. Total time = 3.

Example 2:

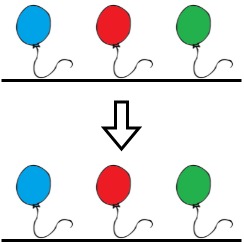
Input: colors = "abc", neededTime = [1,2,3] Output: 0 Explanation: The rope is already colorful. Bob does not need to remove any balloons from the rope.

Example 3:

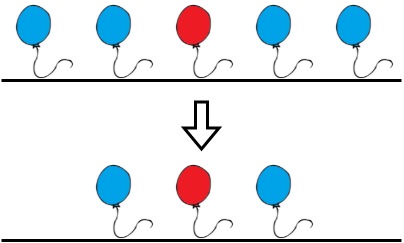
Input: colors = "aabaa", neededTime = [1,2,3,4,1] Output: 2 Explanation: Bob will remove the ballons at indices 0 and 4. Each ballon takes 1 second to remove. There are no longer two consecutive balloons of the same color. Total time = 1 + 1 = 2.

Constraints:

• n == colors.length == neededTime.length
• 1 <= n <= 105
• 1 <= neededTime[i] <= 104
• colors contains only lowercase English letters.

Problem Analysis:

High-Level Strategy:

The solution uses a two-pointer approach to iterate through the colors string and neededTime list. The goal is to minimize the cost of painting the colors. If two consecutive colors are the same, the algorithm compares their corresponding needed times. If the needed time for the color at index l is less than the needed time for the color at index r, the algorithm selects the color at index l, and its needed time is added to the total cost (res). Otherwise, the algorithm selects the color at index r. If the colors are different, the algorithm moves the left pointer (l) to the current right pointer (r). This ensures that the algorithm considers consecutive segments of the same color.

Explanation for l=r: Setting l = r when the colors are different is essential for handling consecutive segments of the same color. When l = r, the algorithm effectively moves the left pointer to the next segment, allowing it to start comparing colors and needed times afresh for the new segment.

Complexity:

• Time Complexity: O(N), where N is the length of the colors string.
• Space Complexity: O(1), as the algorithm uses a constant amount of extra space.

Solutions:

class Solution:
    def minCost(self, colors: str, neededTime: List[int]) -> int:
        # two pointer
        # remove least cost if 2 are same
        l = res = 0
        for r in range(1, len(colors)):
            if colors[l] == colors[r]:
                if neededTime[l] < neededTime[r]:
                    res += neededTime[l]
                    l = r
                else: 
                    res += neededTime[r]
            else:
                l = r
        return res

Similar Questions