1637 Widest Vertical Area Between Two Points Containing No Points - Medium

Problem:

Given n points on a 2D plane where points[i] = [xi, yi], Return the widest vertical area between two points such that no points are inside the area.

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

Example 1:

​

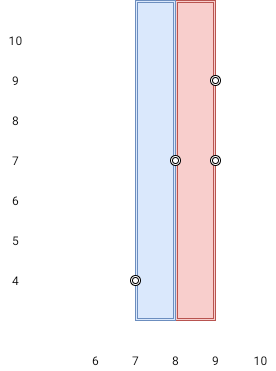
Input: points = [[8,7],[9,9],[7,4],[9,7]] Output: 1 Explanation: Both the red and the blue area are optimal.

Example 2:

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]] Output: 3

Constraints:

• n == points.length
• 2 <= n <= 105
• points[i].length == 2
• 0 <= xi, yi <= 109

Problem Analysis:

The high-level strategy of this solution is to sort the given points based on their x-coordinates. After sorting, it iterates through the sorted points and calculates the difference in x-coordinates between adjacent points. The maximum difference is then returned as the result, representing the maximum width of the vertical area.

• Let n be the number of points.

• Sorting the points based on x-coordinates takes O(nlogn) time.

• Iterating through the sorted points and calculating the difference in x-coordinates between adjacent points takes O(n) time.

Solutions:

class Solution:
    def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x: x[0])
        res = 0
        for p in range(len(points)-2):
            res = max(res, points[p+1][0] - points[p][0])
        return res

Similar Questions