Brand Logo Walter Teng.

1791 Find Center of Star Graph - Easy

Problem:

There is an undirected star graph consisting of n nodes labeled from 1 to n. A star graph is a graph where there is one center node and exactly n - 1 edges that connect the center node with every other node.

You are given a 2D integer array edges where each edges[i] = [ui, vi] indicates that there is an edge between the nodes ui and vi. Return the center of the given star graph.

Example 1:

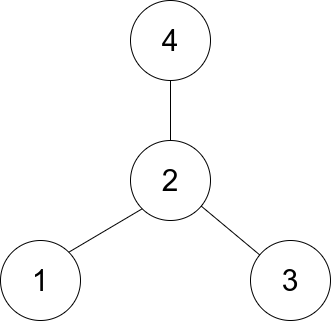
Input: edges = [[1,2],[2,3],[4,2]] Output: 2 Explanation: As shown in the figure above, node 2 is connected to every other node, so 2 is the center.

Example 2:

Input: edges = [[1,2],[5,1],[1,3],[1,4]] Output: 1

Constraints:

  • 3 <= n <= 105
  • edges.length == n - 1
  • edges[i].length == 2
  • 1 <= ui, vi <= n
  • ui != vi
  • The given edges represent a valid star graph.

Problem Analysis:

  1. High-Level Strategy:

    • The problem aims to find the common node in two edges of a graph, which effectively means finding the node shared by both edges.
    • The solution takes advantage of the fact that the common node will exist in both edges.
    • It initializes two variables first and second, representing the first and second edges, respectively, extracted from the edges list.
    • Then, it iterates through the elements of the first edge and checks if each element exists in the second edge.
    • The common node is found by identifying the intersection of elements between the first and second edges.
    • Finally, it returns the first node found in the common list, which represents the common node between the two edges.

  2. Complexity:

    • The initialization of first and second edges takes constant time since they are just references to two elements in the edges list.
    • The list comprehension used to find the common elements between first and second edges has a time complexity of O(n^2), where n is the size of the edges.
    • However, in practice, since the number of nodes in the graph is fixed (typically small), and edges contains only two lists of nodes, the time complexity effectively reduces to O(n).
    • The space complexity is O(n), where n is the number of nodes in the graph, due to the space used to store the common list.

Solutions:

class Solution:
    def findCenter(self, edges: List[List[int]]) -> int:
        first = edges[0]
        second = edges[1]
        common = [item for item in first if item in second]
        return common[0]

Similar Questions