Problem:

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise_._

Example 1:

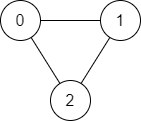
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2 Output: true Explanation: There are two paths from vertex 0 to vertex 2:

• 0 → 1 → 2
• 0 → 2

Example 2:

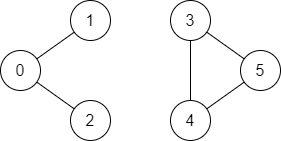
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5 Output: false Explanation: There is no path from vertex 0 to vertex 5.

Constraints:

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• There are no duplicate edges.
• There are no self edges.

Problem Analysis:

This solution uses a Depth-First Search (DFS) algorithm to traverse the graph and find a path from the source node to the destination node. Here's a high-level overview of the strategy:

1. Constructing the Graph: Initially, the code constructs an adjacency list representation of the graph based on the given edges. This representation helps in efficiently traversing the graph.

2. DFS Traversal: The DFS function starts from the source node and explores its neighbors recursively. It marks each visited node to avoid revisiting it to prevent infinite loops. The traversal continues until either the destination node is reached or there are no more unvisited neighbors to explore.

3. Return Result: If the DFS function finds a path from the source to the destination, it returns True, indicating that there exists a valid path. Otherwise, it returns False.

Complexity

• Graph Construction: Constructing the adjacency list takes O(E) time, where E is the number of edges in the graph.

• DFS Traversal: The time complexity of DFS is O(V + E), where V is the number of vertices and E is the number of edges. In the worst case, DFS might visit every node and edge in the graph.

• Space Complexity: The space complexity mainly comes from the adjacency list and the set to track visited nodes. The space complexity is O(V + E) for the adjacency list and O(V) for the visited set, resulting in a total space complexity of O(V + E).

Overall, the solution has a time complexity of O(V + E) and a space complexity of O(V + E), where V is the number of vertices and E is the number of edges in the graph.

Solutions:

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        adj_list = collections.defaultdict(list)

        for u, v in edges:
            adj_list[u].append(v)
            adj_list[v].append(u)

        visited = set()

        def dfs(node):
            if node == destination:
                return True

            visited.add(node)
            for v in adj_list[node]:
                if v not in visited and dfs(v):
                    return True
            return False

        return dfs(source)

Similar Questions