Walter's Leetcode Solutions

Problem:

You are given the root of a full binary tree with the following properties:

Leaf nodes have either the value 0 or 1, where 0 represents False and 1 represents True.
Non-leaf nodes have either the value 2 or 3, where 2 represents the boolean OR and 3 represents the boolean AND.

The evaluation of a node is as follows:

If the node is a leaf node, the evaluation is the value of the node, i.e. True or False.
Otherwise, evaluate the node's two children and apply the boolean operation of its value with the children's evaluations.

Return the boolean result of evaluating the root node.

A full binary tree is a binary tree where each node has either 0 or 2 children.

A leaf node is a node that has zero children.

Example 1:

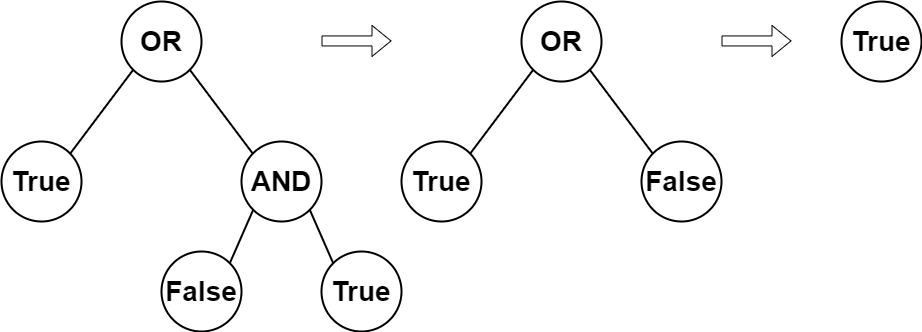
Input: root = [2,1,3,null,null,0,1] Output: true Explanation: The above diagram illustrates the evaluation process. The AND node evaluates to False AND True = False. The OR node evaluates to True OR False = True. The root node evaluates to True, so we return true.

Example 2:

Input: root = [0] Output: false Explanation: The root node is a leaf node and it evaluates to false, so we return false.

Constraints:

The number of nodes in the tree is in the range [1, 1000].
0 <= Node.val <= 3
Every node has either 0 or 2 children.
Leaf nodes have a value of 0 or 1.
Non-leaf nodes have a value of 2 or 3.

Problem Analysis:

1. High-Level Strategy:

The solution employs a recursive approach to evaluate a binary tree based on specific conditions at each node. It begins by checking if the current node has both left and right children. If it does, it further inspects the value of the node. If the value is 2, it evaluates the left and right subtrees using logical OR. If the value is 3, it evaluates the left and right subtrees using logical AND. In cases where the node does not have both children, it returns the value of the node itself. This recursive strategy effectively evaluates the tree based on logical operations determined by the node values.

2. Complexity Analysis:

Time Complexity:

The time complexity of this solution is O(N), where N is the number of nodes in the binary tree. This is because each node is visited once during the traversal, and for each node, there are constant-time operations involved in evaluating the node's value and its children.

Space Complexity:

The space complexity is dependent on the depth of the recursion, which can extend up to the height of the tree. In the worst-case scenario of a completely unbalanced tree, the space complexity could be O(N), where N is the number of nodes. However, in balanced trees, the space complexity would typically be O(log N), where N is the number of nodes, as the recursion stack would not exceed the height of the tree.

Solutions:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def evaluateTree(self, root: Optional[TreeNode]) -> bool:
        if root.left and root.right:
            if root.val == 2:
                return self.evaluateTree(root.left) or self.evaluateTree(root.right)
            elif root.val == 3:
                return self.evaluateTree(root.left) and self.evaluateTree(root.right)
        else:
            return root.val

Walter Teng.