Problem:

You are given an n x n integer matrix grid.

Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:

• maxLocal[i][j] is equal to the largest value of the 3 x 3 matrix in grid centered around row i + 1 and column j + 1.

In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.

Return the generated matrix.

Example 1:

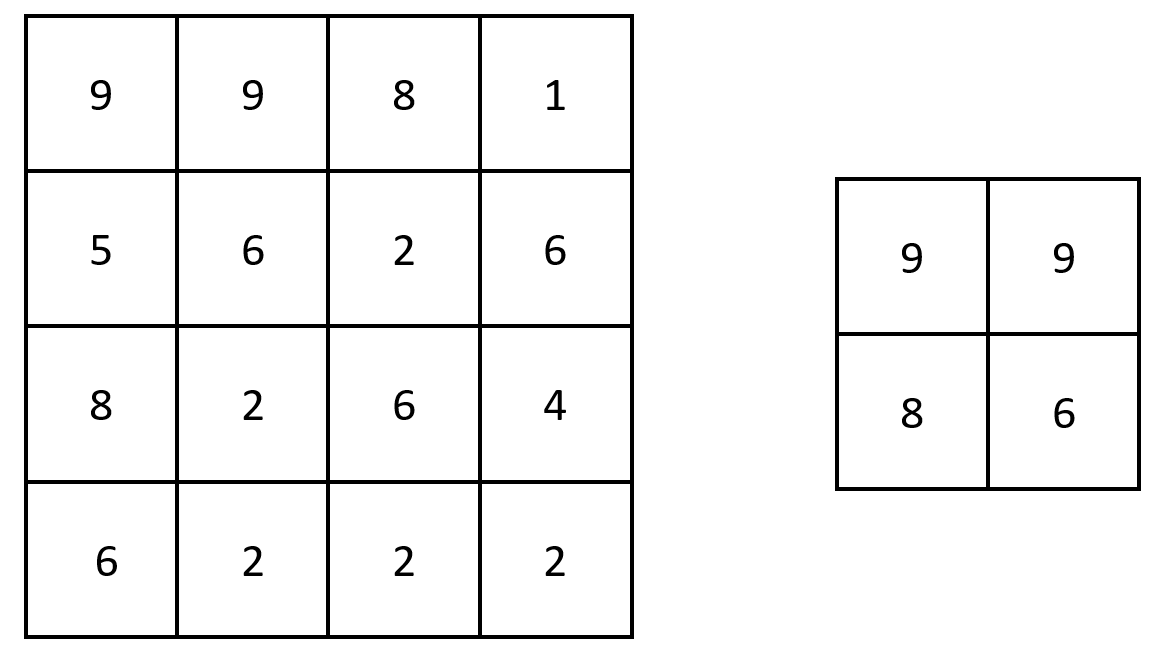
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]] Output: [[9,9],[8,6]] Explanation: The diagram above shows the original matrix and the generated matrix. Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.

Example 2:

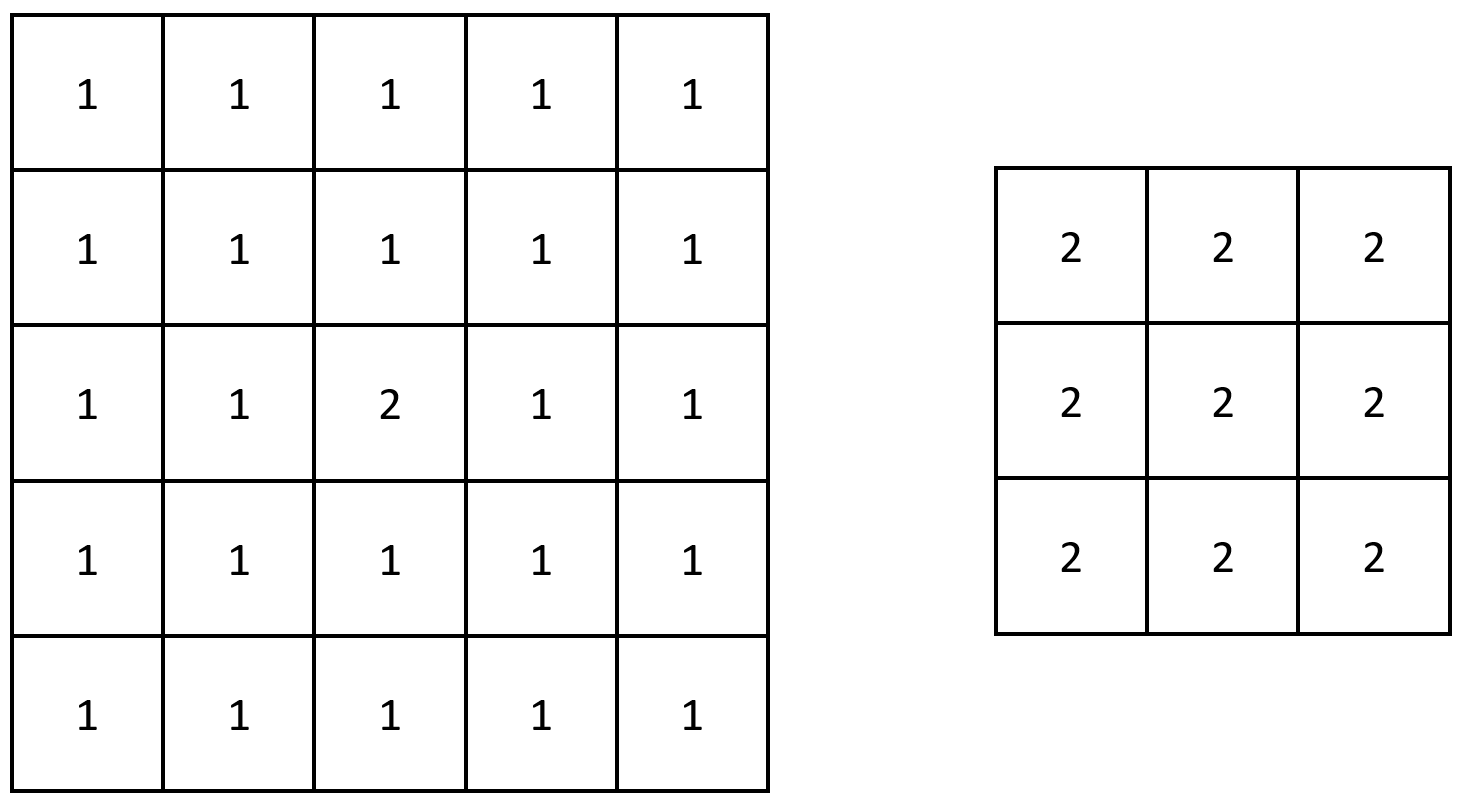
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]] Output: [[2,2,2],[2,2,2],[2,2,2]] Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.

Constraints:

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 1 <= grid[i][j] <= 100

Problem Analysis:

This solution aims to find the largest element in each local 3x3 subgrid within the given grid. The algorithm iterates through each position in the grid, calculates the maximum value within the corresponding 3x3 subgrid centered at that position, and stores it in the result grid.

1. High-level strategy:

   • Iterate through each position (i, j) in the grid.
   • For each position, find the maximum value within the 3x3 subgrid centered at (i, j).
   • Store the maximum value in the result grid at the corresponding position (i, j).

2. Complexity:

   • Let n be the size of the input grid.
   • The nested loops iterate over the positions in the grid, which gives O(n^2) iterations.
   • Within each iteration, there's another nested loop iterating over a fixed 3x3 subgrid, resulting in constant time complexity, O(1).
   • So, the overall time complexity is O(n^2).
   • The space complexity is also O(n^2) since the result grid is of size (n - 2) x (n - 2), which is proportional to the input grid size.

Solutions:

class Solution:
    def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
        n = len(grid)
        result_size = n - 2 
        result = [[0] * result_size for _ in range(result_size)]

        for i in range(result_size):
            for j in range(result_size):
                
                max_val = 0
                for di in range(3):
                    for dj in range(3):
                        max_val = max(max_val, grid[i + di][j + dj])
                result[i][j] = max_val

        return result

Similar Questions