2385 Amount of Time for Binary Tree to Be Infected - Medium

Problem:

You are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.

Each minute, a node becomes infected if:

The node is currently uninfected.
The node is adjacent to an infected node.

Return the number of minutes needed for the entire tree to be infected.

Example 1:

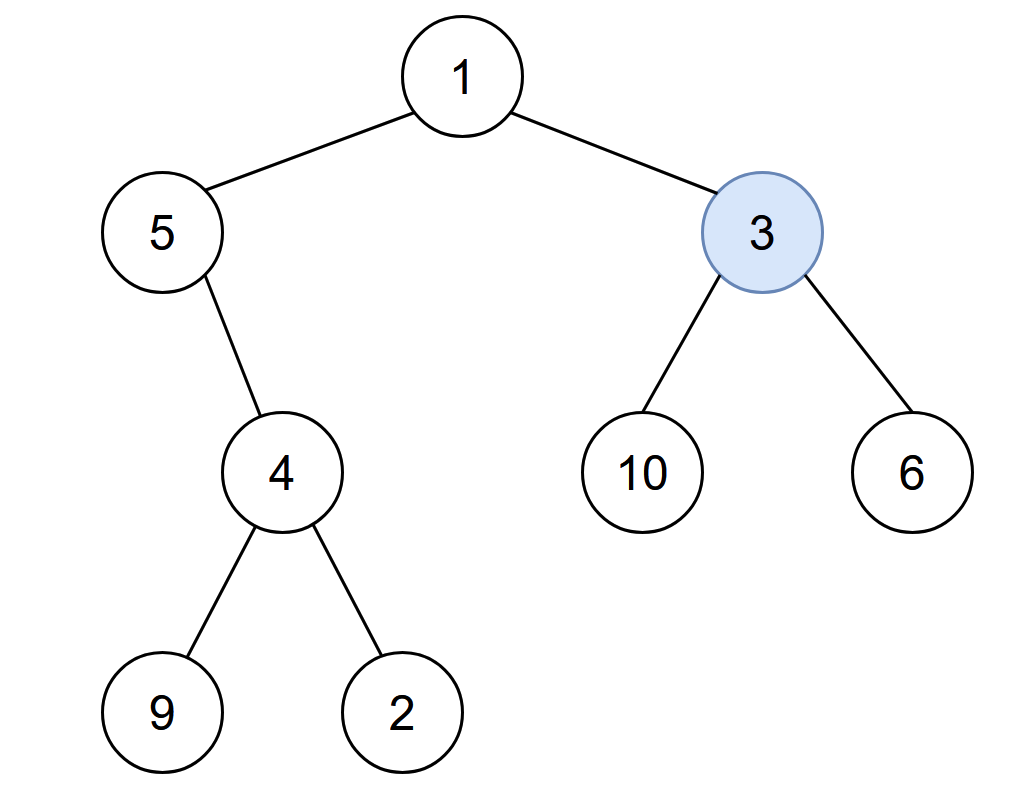
Input: root = [1,5,3,null,4,10,6,9,2], start = 3 Output: 4 Explanation: The following nodes are infected during:

Minute 0: Node 3
Minute 1: Nodes 1, 10 and 6
Minute 2: Node 5
Minute 3: Node 4
Minute 4: Nodes 9 and 2 It takes 4 minutes for the whole tree to be infected so we return 4.

Example 2:

Input: root = [1], start = 1 Output: 0 Explanation: At minute 0, the only node in the tree is infected so we return 0.

Constraints:

The number of nodes in the tree is in the range [1, 105].
1 <= Node.val <= 105
Each node has a unique value.
A node with a value of start exists in the tree.

Problem Analysis:

1. High-Level Strategy:

Elegant Solution from qu1ck

The solution uses a Depth-First Search (DFS) approach to traverse a binary tree and calculate two values for each node:

The maximum depth of the subtree rooted at the current node if it contains the start node.
The time it takes to infect the subtree rooted at the current node if it doesn't contain the start node.

The DFS function (dfs) returns these two values for each node, and based on the conditions, it calculates the time to infect the subtree and the root of the subtree.

The algorithm considers three cases:

If the current node is the start node, it returns the maximum depth of the left and right subtrees plus 1 (for the current node) and 0 (time to infect the root).
If the current node is not the start node, but one of its subtrees contains the start node, it calculates the time to infect the subtree and the root of the subtree.
If neither subtrees have the start node, it returns the maximum depth of the subtrees plus 1 and -1 to indicate the absence of the start node.

The final result is the maximum depth of the entire tree, obtained by calling the DFS function on the root node.

2. Complexity:

Time Complexity: The DFS function visits each node exactly once, and for each node, it performs constant time operations. Therefore, the overall time complexity is O(n), where n is the number of nodes in the binary tree.
Space Complexity: The space complexity is O(h), where h is the height of the binary tree. This is due to the recursive calls in the DFS function, which creates a stack in memory. In the worst case, for a skewed tree, the height h could be equal to the number of nodes n, leading to O(n) space complexity. However, for a balanced tree, the space complexity would be O(log n).

Solutions:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        # Define the DFS (Depth-First Search) function that returns two values:
        # - The maximum depth of the subtree rooted at node n if it contains the start node
        # - The time it takes to infect the subtree rooted at node n if it doesn't contain the start node
        def dfs(n):
            if not n:
                # Base case: Return (-1, -1) for leaf nodes and non-existent nodes
                return -1, -1

            # Recursive calls on left and right subtrees
            d0, t0 = dfs(n.left)
            d1, t1 = dfs(n.right)

            # Check if the current node is the start node
            if n.val == start:
                # Case 1: Current node is the start node
                # Return the maximum depth of left and right subtrees + 1, and 0 (time to infect the root)
                return max(d0, d1) + 1, 0
            else:
                # Case 2: Current node is not the start node but one of the subtrees has it
                # Calculate the time to infect the subtree and the time to infect the root of the subtree
                if t0 >= 0:
                    return max(d1 + 2 + t0, d0), t0 + 1
                if t1 >= 0:
                    return max(d0 + 2 + t1, d1), t1 + 1
                # Case 3: Neither subtrees have the start node
                # Return the maximum depth of subtrees + 1, and -1 to indicate the absence of the start node
                return max(d0, d1) + 1, -1

        # Call the DFS function on the root and return the maximum depth of the entire tree
        return dfs(root)[0]

Walter Teng.