Problem:

You are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.

Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).

The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.

Example 1:

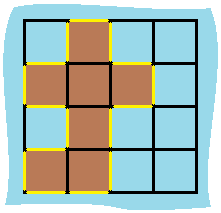
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] Output: 16 Explanation: The perimeter is the 16 yellow stripes in the image above.

Example 2:

Input: grid = 1 Output: 4

Example 3:

Input: grid = 1,0 Output: 4

Constraints:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 100
• grid[i][j] is 0 or 1.
• There is exactly one island in grid.

Problem Analysis:

This solution utilizes depth-first search (DFS) to explore the grid starting from each land cell. Here's a high-level breakdown:

1. Initialization:

   • A set visit is initialized to keep track of visited cells, preventing revisiting.

2. DFS function (dfs):

   • This recursive function traverses the grid from a given cell (i, j).
   • It checks boundaries and water cells, returning 1 for boundary cells or water cells and 0 for visited cells.
   • If the cell is within bounds and land, it marks it as visited, and recursively explores adjacent cells (up, down, left, right).
   • It returns the count of perimeter associated with the current land cell.

3. Main loop:

   • Iterates through every cell in the grid.
   • When a land cell is encountered, it triggers DFS from that cell, accumulating the perimeter count.
   • The loop terminates as soon as it finds the first land cell (as instructed by return dfs(i, j)), which indicates that the whole island's perimeter has been calculated.

Complexity:

• Time complexity:

  • Each cell is visited exactly once, and for each cell, DFS explores its adjacent cells.
  • If the grid has n rows and m columns, the time complexity is O(n * m), where n and m are the dimensions of the grid.

• Space complexity:

  • The additional space complexity comes from the recursion stack and the set visit.
  • In the worst case, if the grid is filled with land cells and no water cells are visited, the recursion depth can be n * m, and the set visit could store n * m cells.
  • Thus, the space complexity is O(n * m).

Overall, this solution provides an efficient way to calculate the perimeter of the island represented by the grid.

Solutions:

class Solution:
    def islandPerimeter(self, grid: List[List[int]]) -> int:
        visit = set()

        def dfs(i, j):
            if i >= len(grid) or j >= len(grid[0]) or i < 0 or j < 0 or grid[i][j] == 0:
                return 1
            if (i, j) in visit:
                return 0
            
            visit.add((i,j))
            perim = dfs(i, j+1)
            perim += dfs(i + 1, j)
            perim += dfs(i, j-1)
            perim += dfs(i-1, j)
            return perim

        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j]:
                    return dfs(i, j)

Similar Questions