872 Leaf-Similar Trees - Easy

Problem:

Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a leaf value sequence*.*

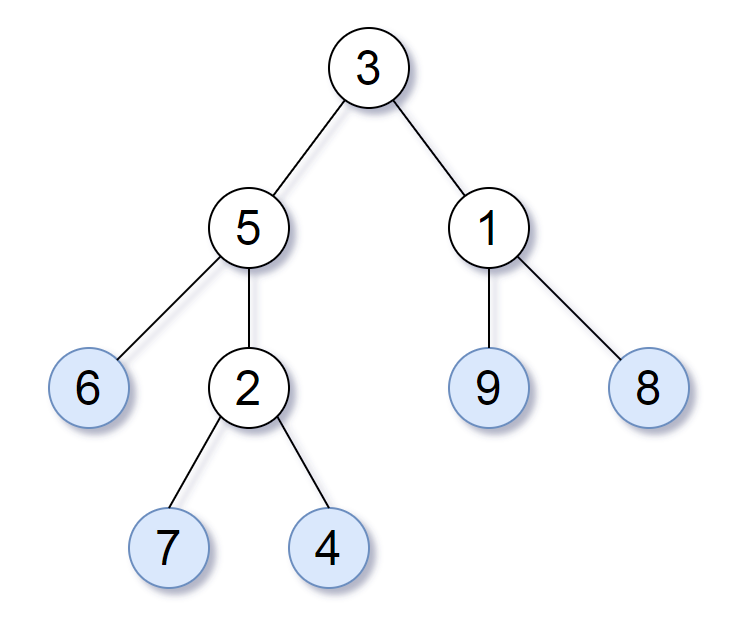
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Example 1:

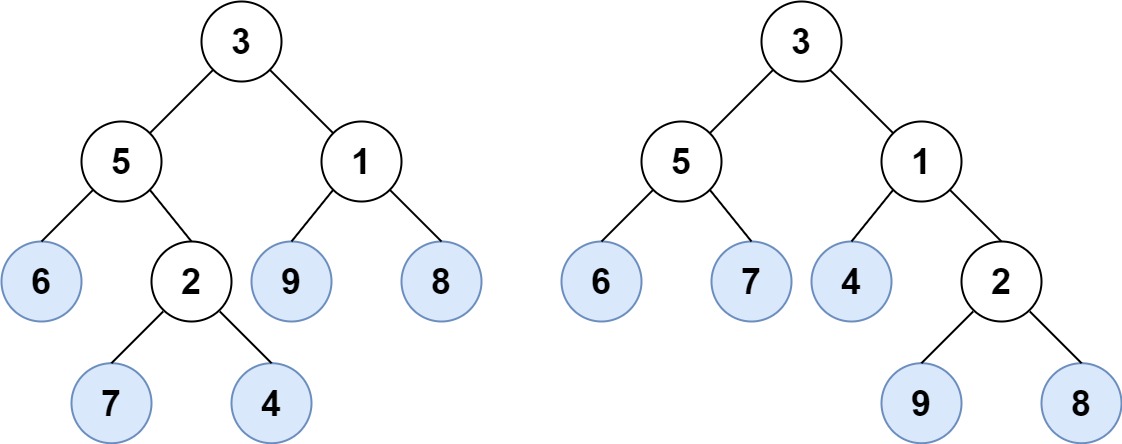
Input: root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8] Output: true

Example 2:

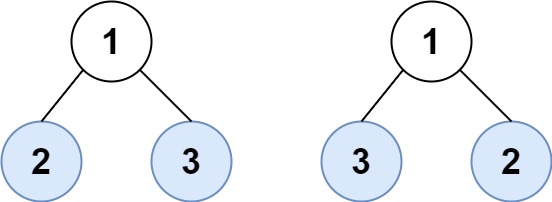
Input: root1 = [1,2,3], root2 = [1,3,2] Output: false

Constraints:

The number of nodes in each tree will be in the range [1, 200].
Both of the given trees will have values in the range [0, 200].

Problem Analysis:

Certainly! Let's discuss the high-level strategy and complexity of the given solution.

1. High-Level Strategy:

The goal of the problem is to check if the leaf sequences of two binary trees (root1 and root2) are similar. Two trees are considered leaf-similar if their leaf nodes, when read from left to right, form the same sequence.

The high-level strategy of the solution involves using Depth-First Search (DFS) to traverse each tree and collect the leaf values in a list. The dfs function recursively traverses the tree, and when a leaf node is encountered (a node with no left or right child), its value is appended to the list of leaves.

After obtaining the lists of leaf values for both trees (leaves1 and leaves2), the solution checks if the lists are equal. If the lists are equal, it means the leaf sequences are similar, and the function returns True; otherwise, it returns False.

2. Complexity:

Time Complexity:
- The time complexity is O(N + M), where N and M are the number of nodes in root1 and root2 respectively.
- Both DFS traversals take linear time to visit each node exactly once. The traversal of each tree contributes O(N) and O(M) time complexity respectively.
- The final comparison of leaf sequences (leaves1 == leaves2) takes O(min(N, M)) time as it compares the lengths of the two lists.
Space Complexity:
- The space complexity is O(H1 + H2), where H1 and H2 are the heights of root1 and root2 respectively.
- The space complexity is dominated by the space required for the recursive DFS calls. In the worst case, when the trees are highly unbalanced, the recursion depth could be equal to the height of the tree.
- The space used by the lists (leaves1 and leaves2) is not considered in the space complexity analysis, as it is dependent on the input and not on the structure of the trees.

Solutions:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def leafSimilar(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool:
        def dfs(root, leaves):
            if not root:
                return
            if not root.left and not root.right:
                leaves.append(root.val)
                return
            dfs(root.left, leaves)
            dfs(root.right, leaves)

        leaves1, leaves2 = [], []
        dfs(root1, leaves1)
        dfs(root2, leaves2)

        return leaves1 == leaves2

Walter Teng.