935 Knight Dialer - Medium

Problem:

The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:

A chess knight can move as indicated in the chess diagram below:

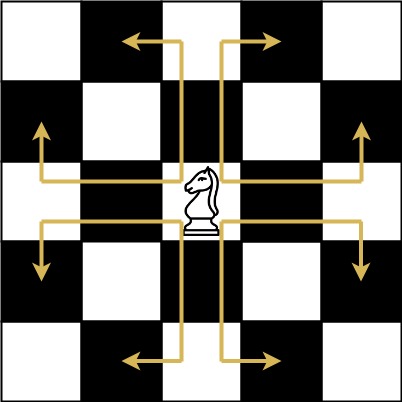
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

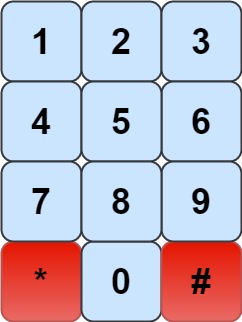
Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 109 + 7.

Example 1:

Input: n = 1 Output: 10 Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

Input: n = 2 Output: 20 Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3131 Output: 136006598 Explanation: Please take care of the mod.

Constraints:

• 1 <= n <= 5000

Problem Analysis:

• see Google Interview Questions Deconstructed: The Knight’s Dialer (Logarithmic Time Edition)

• first, we list out all valid moves for each digit

• then, we initialize the initial state as a list of size 10 for the first moves

• we then loop through the input length (exclude initial state), loop through all 10 digits and all valid moves and update the count in new_dp by adding the count from the previous move dp[move]

• finally we sum up all the counts for all digits.

• Time Complexity:

  • The outer loop runs for n - 1 iterations.
  • The inner loop iterates over all 10 digits, and for each digit, it considers the possible moves defined in the moves dictionary.
  • Therefore, the overall time complexity is O(n) since the number of iterations is directly proportional to the value of n.

• Space Complexity:

  • The space complexity is O(1) since the space used is constant and does not depend on the input size. The main data structures used (dp and new_dp) have fixed sizes.

Solutions:

class Solution:
    def knightDialer(self, n: int) -> int:
        MOD = 10**9 + 7
        moves = {
            1: [6, 8],
            2: [7, 9],
            3: [4, 8],
            4: [3, 9, 0],
            5: [],
            6: [1, 7, 0],
            7: [2, 6],
            8: [1, 3],
            9: [2, 4],
            0: [4, 6]
        }

        dp = [1] * 10
        for _ in range(n - 1):
            new_dp = [0] * 10
            for i in range(10):
                for move in moves[i]:
                    new_dp[i] = (new_dp[i] + dp[move]) % MOD
            dp = new_dp

        return sum(dp) % MOD        

Similar Questions