938 Range Sum of BST

Problem:

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].

Example 1:

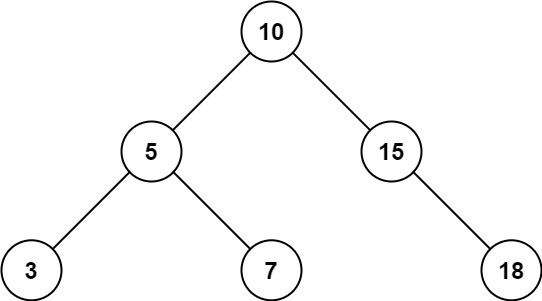
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15 Output: 32 Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2:

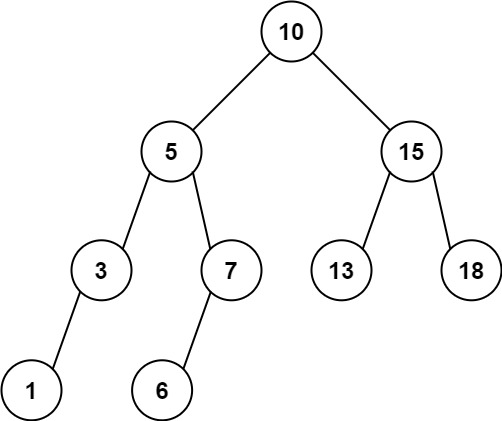
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 Output: 23 Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Constraints:

The number of nodes in the tree is in the range [1, 2 * 104].
1 <= Node.val <= 105
1 <= low <= high <= 105
All Node.val are unique.

Problem Analysis:

1. High-Level Strategy:

The solution is implemented as a recursive algorithm to find the sum of values in a Binary Search Tree (BST) that fall within a given range [low, high]. The idea is to traverse the tree in a depth-first manner. At each node, the algorithm checks whether the node value is within the specified range. Based on this, it decides whether to include the current node's value in the sum and continues the recursive traversal in the left and right subtrees accordingly.

If root.val > high, it means the current node and its right subtree can be ignored, and the search continues in the left subtree.
If root.val < low, it means the current node and its left subtree can be ignored, and the search continues in the right subtree.
If low <= root.val <= high, the current node's value is within the range, and the sum includes the current node's value. The search continues in both the left and right subtrees.

This strategy ensures that only the values within the specified range contribute to the final sum.

2. Complexity:

Let's analyze the time and space complexity of the solution:

Time Complexity:
- The worst-case time complexity is O(N), where N is the number of nodes in the BST. In the worst case, the algorithm may visit all nodes of the tree.
- Each node is visited exactly once, and the work done at each node is constant (simple comparisons and additions).
Space Complexity:
- The space complexity is O(H), where H is the height of the BST.
- In the worst case, the recursion depth is equal to the height of the tree. This is because the algorithm is a depth-first traversal, and the recursion stack keeps track of the path from the root to the current node.
- In a balanced BST, the height is log(N), but in the worst case (unbalanced tree), it could be N.

Overall, the solution is efficient, especially when the tree is balanced. However, it may degrade to O(N) time and space complexity in the worst case when the tree is highly unbalanced.

Solutions:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        if not root:
            return 0
        
        if root.val > high:
            return self.rangeSumBST(root.left, low, high)
        elif root.val < low: 
            return self.rangeSumBST(root.right, low, high)
        else:
            return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)

Walter Teng.